Queremos colocar ![]() retângulos de dimensões
retângulos de dimensões ![]() em uma região convexa
de tal maneira que não ocorra superposições entre os retângulos.
em uma região convexa
de tal maneira que não ocorra superposições entre os retângulos.
Se a região convexa é um retângulo, então o objetivo é encontrar
![]() , onde
, onde ![]() é a coordenada
é a coordenada ![]() do centro do retângulo
do centro do retângulo ![]() e
e ![]() é a
coordenada
é a
coordenada ![]() do centro do retângulo
do centro do retângulo ![]() , resolvendo o problema:
, resolvendo o problema:
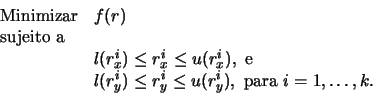
onde ![]() é uma das funções vistas na Seção
é uma das funções vistas na Seção ![]() e
e ![]() é o limitante inferior de
é o limitante inferior de ![]() e
e ![]() é o limitante superior de
é o limitante superior de ![]() .
.
Se a região convexa, definida pela função ![]() , não é um retângulo, então o
objetivo é encontrar
, não é um retângulo, então o
objetivo é encontrar
![]() ,
onde
,
onde ![]() é a coordenada
é a coordenada ![]() do centro do retângulo
do centro do retângulo ![]() e
e ![]() é a
coordenada
é a
coordenada ![]() do centro do retângulo
do centro do retângulo ![]() , resolvendo o problema:
, resolvendo o problema:
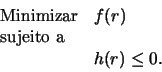
Que pode ser alterada para que, caso ![]() seja positiva, a função sofra uma
penalidade. Assim, podemos resolver o problema:
seja positiva, a função sofra uma
penalidade. Assim, podemos resolver o problema:
Se o valor da função objetiva no minimizador global desses problemas é zero então a resposta do problema de decisão é SIM, caso contrário, a resposta é NÃO.
Observe que os problemas descritos acima são problemas de otimização contínua onde a função objetiva tem a primeira derivada contínua.