Antes de mostrar os modelos, vamos definir o que são sentinelas, pois em alguns métodos são necessários o uso deles.
Um conjunto de sentinelas é um conjunto mínimo de pontos de um retângulo,
tal que se dois retângulos ![]() e
e ![]() se intersectam, então ocorre pelo
menos uma das seguintes situações:
se intersectam, então ocorre pelo
menos uma das seguintes situações:
A Figura ![]() é um exemplo de um conjunto de sentinelas
de um retângulo.
é um exemplo de um conjunto de sentinelas
de um retângulo.
Agora que já definimos o que são sentinelas, vamos mostrar os modelos contínuos.
Método do Vetor
Esse método usa sentinelas.
Para verificar se ocorre intersecção entre dois retângulos ![]() e
e ![]() , devemos verificar para todos os sentinelas do retângulo
, devemos verificar para todos os sentinelas do retângulo
![]() , se existe ao menos um deles no interior do retângulo
, se existe ao menos um deles no interior do retângulo ![]() e verificar para todos os sentinelas do retângulo
e verificar para todos os sentinelas do retângulo ![]() , se existe
ao menos um deles no interior do retângulo
, se existe
ao menos um deles no interior do retângulo ![]() .
.
Para aplicar o método devemos, antes de verificar se um sentinela de
um retângulo está no interior do outro retângulo, levar o retângulo para a
origem. Seja ![]() a coordenada do vértice inferior
esquerdo do retângulo e
a coordenada do vértice inferior
esquerdo do retângulo e ![]() a coordenada do sentinela.
Para levar o retângulo para a origem é só subtrair sua coordenada
pelo vetor
a coordenada do sentinela.
Para levar o retângulo para a origem é só subtrair sua coordenada
pelo vetor ![]() . Também devemos subtrair a coordenada do
sentinela por esse vetor. Note que a coordenada do retângulo,
depois de subtraído pelo vetor, será sempre
. Também devemos subtrair a coordenada do
sentinela por esse vetor. Note que a coordenada do retângulo,
depois de subtraído pelo vetor, será sempre ![]() (origem),
portanto não é necessário subtrair o vetor da coordenada do
retângulo, apenas será necessária subtrair o vetor da coordenada
do sentinela, assim a nova coordenada do sentinela será
(origem),
portanto não é necessário subtrair o vetor da coordenada do
retângulo, apenas será necessária subtrair o vetor da coordenada
do sentinela, assim a nova coordenada do sentinela será
![]() .
.
Após feito isso, podemos considerar que o retângulo, de dimensão ![]() ,
tem dois vetores
,
tem dois vetores ![]() e
e ![]() , onde
, onde ![]() e
e ![]() , e se o
retângulo
, e se o
retângulo ![]() está deitado então
está deitado então ![]() e
e ![]() , e se o retângulo
, e se o retângulo
![]() está em pé então
está em pé então ![]() e
e ![]() (como mostra a Figura
(como mostra a Figura
![]() ). Assim a nova coordenada
). Assim a nova coordenada ![]() do sentinela
pode ser representada através da seguinte equação linear:
do sentinela
pode ser representada através da seguinte equação linear:
onde
![]() .
.
Se
![]() e
e ![]() então o sentinela está
no interior do retângulo. Portanto os retângulos se intersectam.
então o sentinela está
no interior do retângulo. Portanto os retângulos se intersectam.
Resolvendo a equação temos que:
A função contínua e diferenciável que mede a superposição entre os retângulos e seu gradiente para esse método são:
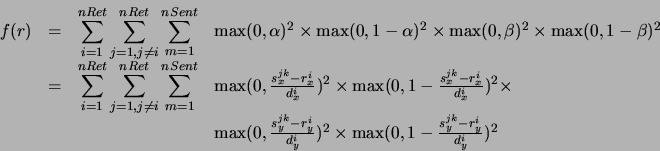
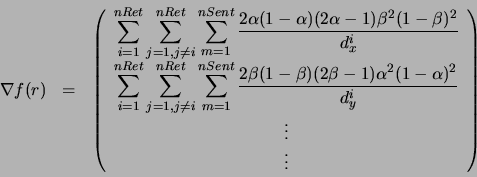
onde
![]() e
e ![]() é a coordenada inferior esquerda
é a coordenada inferior esquerda ![]() do retângulo
do retângulo ![]() e
e ![]() é a
coordenada inferior esquerda
é a
coordenada inferior esquerda ![]() do retângulo
do retângulo ![]() .
. ![]() é a
coordenada
é a
coordenada ![]() do sentinela
do sentinela ![]() do retângulo
do retângulo ![]() e
e ![]() é a
coordenada
é a
coordenada ![]() do sentinela
do sentinela ![]() do retângulo
do retângulo ![]() . E
. E ![]() é o número
de retângulos e
é o número
de retângulos e ![]() é o número de sentinelas.
é o número de sentinelas.
Essa função vale zero se não existe superposição entre os retângulos e qualquer valor positivo se existe superposição entre os retângulos.
Método das Restrições
Esse método usa sentinelas.
Para verificar se ocorre intersecção entre dois retângulos ![]() e
e ![]() , devemos verificar para todos os sentinelas do retângulo
, devemos verificar para todos os sentinelas do retângulo
![]() , se existe ao menos um deles no interior do retângulo
, se existe ao menos um deles no interior do retângulo ![]() e verificar para todos os sentinelas do retângulo
e verificar para todos os sentinelas do retângulo ![]() , se existe
ao menos um deles no interior do retângulo
, se existe
ao menos um deles no interior do retângulo ![]() .
.
Podemos considerar que os lados do retângulo ![]() , de dimensão
, de dimensão ![]() ,
são quatro restrições lineares (como mostra a Figura
,
são quatro restrições lineares (como mostra a Figura ![]() ).
Sejam
).
Sejam ![]() a coordenada de um sentinela do retângulo
a coordenada de um sentinela do retângulo ![]() e
e
![]() e
e ![]() as dimensões do retângulo
as dimensões do retângulo ![]() , onde se o retângulo
está deitado então
, onde se o retângulo
está deitado então ![]() e
e ![]() , e se o retângulo está em pé
então
, e se o retângulo está em pé
então ![]() e
e ![]() .
.
Assim se:
então o sentinela está no interior do retângulo. Portanto os retângulos se intersectam.
A função contínua e diferenciável que mede a superposição entre os retângulos e seu gradiente para esse método são:
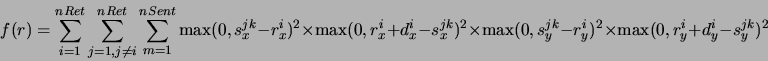
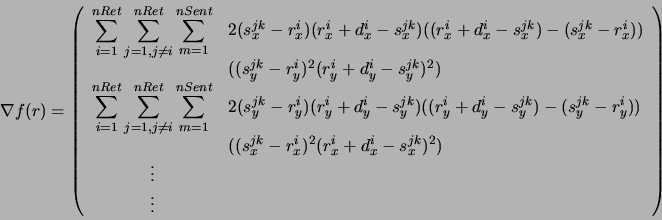
onde
![]() e
e ![]() é a coordenada inferior esquerda
é a coordenada inferior esquerda ![]() do retângulo
do retângulo ![]() e
e ![]() é a
coordenada inferior esquerda
é a
coordenada inferior esquerda ![]() do retângulo
do retângulo ![]() .
. ![]() é a
coordenada
é a
coordenada ![]() do sentinela
do sentinela ![]() do retângulo
do retângulo ![]() e
e ![]() é a
coordenada
é a
coordenada ![]() do sentinela
do sentinela ![]() do retângulo
do retângulo ![]() . E
. E ![]() é o número
de retângulos e
é o número
de retângulos e ![]() é o número de sentinelas.
é o número de sentinelas.
Essa função vale zero se não existe superposição entre os retângulos e qualquer valor positivo se existe superposição entre os retângulos.
Método da Distância do Centros
Esse método NÃO usa sentinelas.
Considere dois retângulos ![]() e
e ![]() de dimensões
de dimensões ![]() , onde
as coordenadas do centro do retângulo são
, onde
as coordenadas do centro do retângulo são
![]() e
e
![]() respectivamente. Sejam
respectivamente. Sejam ![]() e
e ![]() as dimensões
do retângulo
as dimensões
do retângulo ![]() e
e ![]() e
e ![]() as dimensões do retângulo
as dimensões do retângulo ![]() ,
onde se o retângulo está deitado então
,
onde se o retângulo está deitado então ![]() e
e ![]() , e se o
retângulo está em pé então
, e se o
retângulo está em pé então ![]() e
e ![]() (Veja Figura
(Veja Figura ![]() ).
).
Assim se:
então os retângulos se intersectam. Caso contrário, os retângulos não se intersectam.
A função contínua e diferenciável que mede a superposição entre os retângulos e seu gradiente para esse método são:
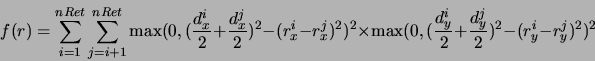
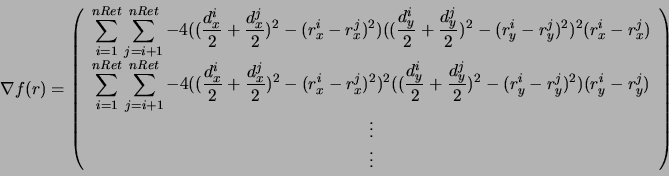
onde
![]() e
e ![]() é a coordenada
é a coordenada ![]() do centro do retângulo
do centro do retângulo ![]() e
e ![]() é a coordenada
é a coordenada
![]() do dentro do retângulo
do dentro do retângulo ![]() . E
. E ![]() é o número de retângulos.
é o número de retângulos.
Essa função vale zero se não existe superposição entre os retângulos e qualquer valor positivo se existe superposição entre os retângulos.
Método da Circunferência
Esse método serve para gerar uma configuração inicial dos retângulos
para os outros métodos. Pegamos algumas circunferências que cobre
quase todo o retângulo, como mostra a Figura ![]() . Esse
método é citado em [7] para o empacotamento de cilindros.
. Esse
método é citado em [7] para o empacotamento de cilindros.
Para gerar essa configuração inicial, devemos verificar para todas as circunferências de um retângulo se não existe intersecção com as outras circunferências dos outros retângulos.
Considere duas circunferências ![]() e
e ![]() , onde as coordenadas do
centro são
, onde as coordenadas do
centro são
![]() e
e
![]() e os raios são
e os raios são ![]() e
e ![]() , respectivamente. (Veja Figura
, respectivamente. (Veja Figura ![]() )
)
Assim se:
então os retângulos se intesectam.
A função contínua e diferenciável que mede a superposição entre os retângulos e seu gradiente para esse método são:
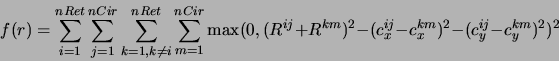
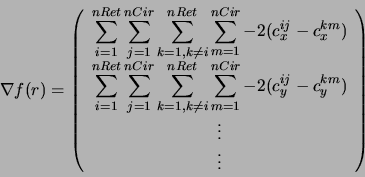
onde
![]() e
e ![]() é a coordenada
é a coordenada ![]() do centro do retângulo
do centro do retângulo ![]() e
e ![]() é a coordenada
é a coordenada
![]() do centro do retângulo
do centro do retângulo ![]() .
. ![]() é a coordenada
é a coordenada ![]() do
centro da circunferência
do
centro da circunferência ![]() do retângulo
do retângulo ![]() e
e ![]() é a
coordenada
é a
coordenada ![]() do centro da circunferência
do centro da circunferência ![]() do retângulo
do retângulo ![]() .
.
![]() é o raio da circunferência
é o raio da circunferência ![]() do retângulo
do retângulo ![]() e
e
![]() é o raio da circunferência
é o raio da circunferência ![]() do retângulo
do retângulo ![]() . E
. E ![]() é o número de retângulos e
é o número de retângulos e ![]() é o número de circunferências que
cobrem o retângulo.
é o número de circunferências que
cobrem o retângulo.
Essa função vale zero se não existe superposição entre as circunferências dos retângulos e qualquer valor positivo se existe superposição entre as circunferências e portanto os retângulos se intersectam.