Os métodos descritos anteriormente são chamados de passos únicos ou simples, pois somente
a informação do passo anterior é utilizada para o cálculo do próximo passo.
Adams Moulton utiliza o fato de que iterações (com algum dos outros métodos
para os primeiros passos) anteriores já foram realizadas, isto é, será
necessário guardar as informações dos valores pré calculados de ![]() , com isto
é construido um polinômio que aproxima a derivada da função e consegue-se
extrapolar para o próximo intervalo.
, com isto
é construido um polinômio que aproxima a derivada da função e consegue-se
extrapolar para o próximo intervalo.
O número de iterações anteriores a ser utilizadas determinará o grau do polinômio, sendo assim a ordem do método será o grau do polinômio + 1.
Foi implementado um Adams-Moulton de ![]() ordem, preditor e corretor:
ordem, preditor e corretor:
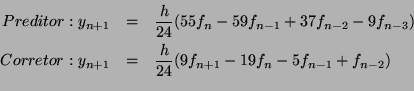
Sendo que:
![]() são os valores da função
calculadas utilizando alguma das técnicas de passo único, nos primeiros passos,
e daí por diante os valores das 4 iterações anteriores são armazenadas.
são os valores da função
calculadas utilizando alguma das técnicas de passo único, nos primeiros passos,
e daí por diante os valores das 4 iterações anteriores são armazenadas.
Este método tem algumas vantagens em relação aos anteriores pois usando o fato
que já temos alguns passos calculados, para conseguir uma precisão equivalente
ao Runge-Kutta ![]() ordem precisaremos apenas calcular duas vezes a função,
ao invés de 4 vezes como no Runge-Kutta.
ordem precisaremos apenas calcular duas vezes a função,
ao invés de 4 vezes como no Runge-Kutta.