Física

Para derivar o coeficiente de difusão do material com base na simulação, serão utilizadas a primeira lei de Fick e a equação para o deslocamento quadrático médio de Einstein.

A primeira lei de Fick relaciona o fluxo de partículas $J$ com o gradiente molar de concentração $\nabla \phi$: $J = -D \nabla \phi$, onde $D$ representa o coeficiente de difusão.

Já a equação de Einstein relaciona o deslocamento quadrático médio $\langle x^2 \rangle$ com o coeficiente de difusão $D$ e o tempo $t$ decorrido desde o estado inicial do sistema: $\langle x^2 \rangle = 6Dt$.

Com base nos dados obtidos e no coeficiente de difusão calculado, será aplicada a lei de Stokes-Einstein para derivar a viscosidade do material. Esta lei, juntamente com a primeira lei de Fick, permite derivar a seguinte relação entre o coeficiente de difusão e a viscosidade $\eta$ do meio: $D = \frac{kT}{6\pi\eta a}$, onde $T$ é a temperatura e $k$ é a constante de Boltzmann.

Para gerar um estado inicial compatível com a realidade, será utilizada a distribuição de Maxwell [3] para estimar um módulo de velocidade inicial para cada molécula com base na temperatura fornecida.

A distribuição de Maxwell é dada por 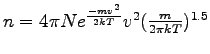$n = 4 \pi N e^{\frac{-mv^2}{2kT}} v^2 (\frac{m}{2 \pi kT})^{1.5}$, onde $n$ é o número de moléculas esperado para a temperatura $T$ numa velocidade $v$, $N$ é o número total de moléculas do meio considerado, $m$ é a massa de cada partícula e $k$ é a constante de Boltzmann.

Como a distribuição de Maxwell fornece o número de moléculas numa determinada velocidade, para estimar a velocidade de uma molécula é necessário calcular o inverso desta distribuição e integrá-lo. Como esta função não admite uma inversa explícita, é necessário fazer tanto a inversão como a integração de modo numérico.