Algoritmos Aproximados para o
Problema do Corte Circular Restrito
Motivação
O problema que este trabalho se propôs a estudar pode ser descrito como o "Empacotamento de Círculos de Tamanho Variado em um Retângulo",
ou ainda "Problema do Corte Circular Restrito".
Os dois nomes se referem às duas motivações ligeiramente distintas que se
pode ter para o problema. No primeiro caso, a motivação pode ser ilustrada com a seguinte situação: uma empresa de transportes despacha
uma variedade de tubos de plástico em containers. O comprimento de cada tubo é o
mesmo do container. Tubos de diferentes diâmetros podem ser encaixados uns
dentro dos outros. Sob a perspectiva da seção transversal de um tal carregamento, temos o
problema bidimensional do empacotamento de círculos dentro de um retângulo. A
questão do encaixe de tubos uns dentro dos outros não é abordada aqui, e
assume-se que já tenhamos a lista dos raios dos tubos
exteriores (círculos) em questão.
A segunda descrição sugere o problema de cortar uma chapa retangular no maior
número possível de círculos tais como descritos por um conjunto dado. Como a
lista de círculos é determinada a priori, temos o caso restrito dos
cortes circulares.
De todo modo, podemos expressar o problema de empacotar círculos de raios
variados em um retângulo como um problema de
programação não-linear, tal como fizemos abaixo (vide
[George95] e
[Hifi04]). Os algoritmos abordados visam resolver o problema de
como encaixar da melhor maneira possível um dado número de círculos dentro de
um dado retângulo - note-se que não será abordado o problema de como alocar os
círculos de modo a minimizar a quantidade de retângulos, caso não caibam em um
apenas.
Seja I o conjunto de índices dos n círculos que são candidatos a serem
empacotados no retângulo R, de dimensões W x L, e seja i um elemento genérico
deste conjunto. Seja ri o raio do i-ésimo círculo. Embora possa haver
diversos círculos de mesmo raio, cada um é indexado separadamente. Não há
relação de ordem definida em função dos índices de I. para cada i pertencente a
I, utilizamos ci para representar o "benefício" de ter o círculo i
colocado dentro do retângulo R. Estes ci's são usados como os
coeficientes da função objetivo na formulação, e seu valor numérico depende do
contexto no qual o problema está sendo resolvido, como exemplificado abaixo.
Em resumo, temos:

Utilizando a letra grega delta para designar a variável de decisão (inteira)
referente à presença do círculo no retângulo, e as letras x e y para designar a
posição do centro de cada um dos círculos, podemos formular o problema como:
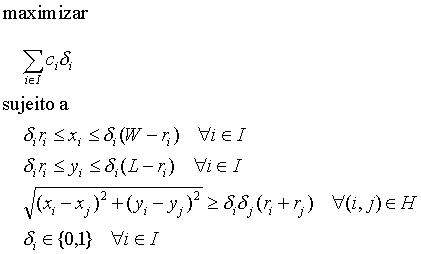
Uma vez que o conjunto I contém n círculos, esta formulação envolve n
variáveis de decisão binárias, 2n variáveis de decisão contínuas e 2n +
½n(n-1) restrições. As duas primeiras restrições garantem que
os círculos presentes em R não ultrapassam as dimensões do retângulo; a
restrição seguinte garante que os círculos não se sobrepõem uns aos outros, e a
última restrição indica que as varíaveis de decisão sobre a presença ou ausência
dos círculos em R é binária.
Cabe observar que esta formulação indica a existência de diversas
configurações que resultam em um mesmo valor da função objetivo, diferindo
apenas no padrão de distribuição dos círculos. Além disto, devido às varíaveis
de decisão inteiras, o espaço de soluções é descontínuo. É importante notar
também que o problema exibe muitos ótimos locais, e em muitos casos um ótimo
global é relativamente raro quando comparado ao número de soluções sub-ótimas
presentes.
Algoritmos de Aproximação
Trata-se de um problema de estrutura muito complexa e difícil de resolver
mesmo para valores pequenos de n. Ele é demonstradamente NP-difícil, conforme
descrito por Lenstra e Ronnooy Kan, em 1979. Assim, ao longo do tempo foram sugeridas algumas
heurísticas e os correspondentes algoritmos. Em
[George95] encontramos a descrição
de 6 destas heurísticas:
- SAMEPACK: abordagem construtiva, em que círculos de tamanho semelhante são
colocados próximos uns aos outros. Em um segundo momento, os círculos são
"afastados" em direção às bordas, procurando uma acomodação que deixe mais
espaços. Diversas configurações são geradas e comparadas.
- WALLPACK: os círculos são distribuídos, do maior para o menor, nos cantos
do retângulo e, em seguida, nas bordas do mesmo. Uma segunda fase semelhante
ao SAMEPACK é realizada, com o processo adicional de simular um
"chacoalhamento" dos círculos para melhor acomodação. Diversas configurações
são geradas e comparadas.
- STABLE1: os círculos são colocados no "fundo" do retângulo, do maior para
o menor, e em seguida em cima de círculos previamente colocados, em uma
pirâmide que busca estabilidade de disposição.
- STABLE2: semelhante ao anterior, mas sem a restrição de colocar apenas
círculos menores sobre maiores, graças a uma análise intermediária dentre as
peças remanescentes, em busca das melhores disposições.
- RANDOM: heurística em que a ordem inicial dos círculos ainda é mantida do
maior para o menor, mas as posições iniciais de cada um é escolhida
aleatoriamente. Testes revelam grande eficiência deste método.
- GENETIC: um algoritmo genético (vide
Algoritmos Genéticos, em
Teoria), partindo de configurações iniciais geradas
por RANDOM, produz soluções adicionais. Altamente eficiente, comprovada
empiricamente.
Em [Hifi04] encontramos mais duas
heurísticas, como se segue:
- CH (Constructive Heuristics): baseada em uma
Abordagem Construtiva, determina uma configuração a partir de uma
ordenação inicial das peças.
- GA-BH (Genetic Algorithm-based Heuristics): baseada em um
Algoritmo Genético para a geração
da ordenação de peças, que a seguir é distribuída no retângulo pela mesma
Abordagem Construtiva definida anteriormente.
Este trabalho visa implementar as duas heurísticas descritas no trabalho de
Hifi et al, expostas acima.

![]()