Problemas de otimização combinatória podem ser definidos, de maneira geral, da seguinte forma: dado um conjunto finito S e uma função custo definida neste conjunto, encontrar um elemento de S que minimize (maximize) esta função. O conjunto S é geralmente dado implicitamente, através das propriedades que seus elementos devem satisfazer. Embora finito, tal conjunto pode ser muito grande, de modo que algoritmos exaustivos para resolver o problema não são viáveis computacionalmente.
Para muitos problemas de otimização combinatória conhecemos algoritmos eficientes. Para muitos outros não conhecemos tais algoritmos. Muitos destes são de grande importância prática, como é o caso do problema de Steiner em grafos e do problema de Steiner com grupos, que são importantes no desevolvimento de circuitos VLSI.
A maioria dos processadores usados atualmente são fabricados com a tecnologia de circuitos integrados VLSI (very-large-scale integration). A confecção de um circuito VLSI é composta de várias fases, dentre as quais duas são de especial importância: a fase de colocação (placement) e a fase de roteamento (routing). Durante a fase de colocação os vários componentes são dispostos na placa de circuito. Estes componentes variam de simples portas lógicas até complexos circuitos. Após a fase de colocação temos a fase de roteamento, durante a qual nosso objetivo é conectar os diversos componentes através de redes condutoras.
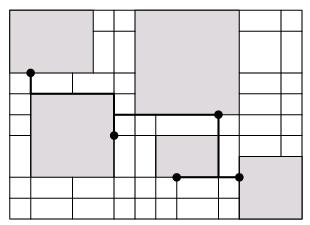
O modelo apropriado para o problema do roteamento é o modelo da rede retilinear. Uma rede retilinear é um grafo cujos vértices são identificados com pontos no plano e cujas arestas são identificadas com segmentos verticaisou horizontais que ligam pontos no plano. A cada aresta também temos um custo associado, que pode ser o comprimento do segmento que ela representa ou outra grandeza apropriada. Observe que, mesmo que as arestas tenham custo igual a seu comprimento, a distância entre dois vértices do grafo não necessariamente é igual à distância retilinear entre os dois pontos no plano: podemos ter "buracos" no grafo, representando regiões do circuito não disponíveis para o roteamento. A Figura 1 apresenta um exemplo de uma rede retilinear.

Dada uma rede retilinear representando um circuito, sabemos quais são os vértices que queremos ligar através da rede condutora. Nosso problema é então o de determinar qual a rede condutora de menor custo que conecta todos os componentes entre si. No caso em que as arestas tem custo igual ao comprimento dos segmentos que representam, queremos encontrar uma rede de menor comprimento possível. O problema de Steiner em grafos é uma generalização do problema que acabamos de descrever para redes retilineares. Dados um grafo G e um conjunto Z de vértices de G, um conjunto S de arestas de G será chamado de Z-gerador se G[S] contém um caminho entre cada par de vértices de Z. Com isso, podemos apresentar o problema de Steiner em grafos.
Problema PSG(G, Z, c): Dados um grafo G, um conjunto Z de vértices de G e um custo racional não-negativo c(e) para cada aresta e de G, encontrar um conjunto S de arestas Z-gerador que minimiza c(S) := soma dos custos das arestas de S.
Chamamos os vértices de Z de terminais e os demais vértices de não-terminais ou vértices de Steiner.
O PSG já foi amplamente estudado [Fer89, HRW92] e é bastante utilizado para modelar problemas de roteamento. Ele não leva em conta, entretanto, um fator adicional que poderia nos permitir obter soluções mais baratas para o problema do roteamento. Observe pela Figura 1 que cada componente pode ser rotacionado ou espelhado após sua localização ter sido determinada. Através de rotações e espelhamentos, a posição do pino conector de um componente pode variar. Para cada possível localização dos pinos, temos uma solução ótima diferente para o PSG. É razoável então querer obter a melhor dentre todas tais soluções.
Foi neste contexto que Reich e Widmayer [RW90] introduziram o problema de Steiner com grupos. Para definirmos o problema, considere um grafo G e uma coleção R de subconjuntos de V(G). Dizemos que um conjunto S de arestas de G é R-gerador se G[S] contém um componente conexo com pelo menos um vértice de cada conjunto de R. Com isso, o problema de Steiner com grupos é o seguinte:
Problema PSGRP(G, R, c): Dados um grafo G, uma coleção R de subconjuntos de V(G) e um custo c(e) para cada aresta e de G, encontrar um conjunto S de arestas R-gerador que minimiza c(S).
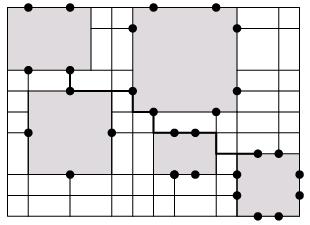
Chamamos os conjuntos de R de grupos. Se um vértice de G pertence a algum grupo ele é um vértice de grupo. Caso contrário, ele é um não-terminal ou vértice de Steiner. Podemos modelar o problema do roteamento da Figura 1 usando o problema de Steiner com grupos, bastando considerar para cada componente um grupo contendo os possíveis conectores daquele componente, considerando-se todas as rotações e espelhamentos. A Figura 2 mostra o resultado obtido. Observe que conseguimos um roteamento de custo menor.
O PSG é NP-difícil [Kar72] e, como este é caso particular do PSGRP, este também é NP-difícil.
Embora o PSGRP seja NP-difícil, sendo que é improvável que existam algoritmos eficientes para resolvê-lo, encontrar soluções ótimas para o problema não deixa de ser importante.
Nosso objetivo é implementar um algoritmo baseado na estratégia branch-and-cut para o problema. Vamos utilizar os conhecimentos adquiridos durante a iniciação científica (que teve início em agosto de 2001). Algoritmos baseados na estratégia branch-and-cut têm se mostrado muito eficazes na resolução de instâncias reais de problemas difíceis de otimização combinatória.
Já dispomos de um algoritmo similiar para o problema de Steiner e de alguns resultados poliédricos para uma formulação específica do problema de Steiner com grupos. Também dispomos de um código inicial do programa que pretendemos desenvolver e estamos no momento escrevendo o módulo de reduções. Pretendemos concluir uma versão completa (mas preliminar) do programa até outubro de 2003. Vamos então aperfeiçoar o código nos meses seguintes.
Na monografia, planejamos incluir os seguintes tópicos:
Na segunda parte, incluiremos os tópicos dispostos na página da disciplina, abordando a integração do curso com o trabalho desenvolvido, as frustrações, etc...
| [Fer89] | C. E. Ferreira, O problema de Steiner em grafos: Uma abordagem poliédrica. Dissertação de mestrado, IME-USP, 1989. | |
| [HRW92] | F. K. Hwang, D. S. Richards e P. Winter. The Steiner Tree Problem, volume 53 de Annals of Discrete Mathematics. North-Holland, 1992. | |
| [Kar72] | R. M. Karp. Reducibility among combinatorial problemas. In Miller e Thatcher, editores, Complexity of Computer Computations, p. 85-103. Plenum Press, New York, 1972. | |
| [RW90] | G. Reich e P. Widmayer. Beyond Steiner's problem: A VLSI oriented generalization. In Graph-Theoretic Concepts in Computer Science WG89, volume 411 de Lecture Notes in Computer Science, p. 196-210. Springer, 1990. |