Algoritmos Utilizados

          Os três principais critérios levados em conta em qualquer algoritmo de desenho de grafos são o número de cruzamentos entre as arestas , o comprimento das arestas e o número de ``dobras'' das arestas , que devem ser o menor possível.

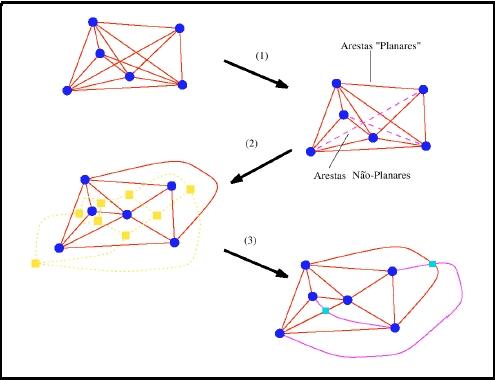
          O algoritmo implementado neste programa dá maior ênfase à minimização dos cruzamentos entre arestas. Encontrar o número mínimo de cruzamentos ou um subgrafo planar máximo é um problema NP-Completo. Os algoritmos de planarização existentes usam heurística. Um método de planarização simples que usa como uma subrotina um algoritmo para encontrar um subgrafo planar trabalha como segue:

  1. Encontre um subgrafo planar S do grafo de entrada G, e particione as arestas em "planares" e "não-planares" ;
  2. Desenhe o subgrafo planar encontrado;
  3. Adicione as arestas não-planares" , uma de cada vez, minimizando o número de cruzamentos introduzidos.
          A figura 7 ilustra o algoritmo utilizado.

Figura 7: Ilustração do Algoritmo Usado.

          No passo 3 do algoritmo acima, inserir uma certa aresta (u,v), é equivalente a encontrar um caminho mais curto no grafo corrente da face incidente em u para a face incidente em v.

          Uma heurística simples para o passo 1, encontrar o grafo planar máximo S do grafo de entrada G, é como segue:

  1. Comece com um subgrafo S consistindo somente dos vértices de G, mas nenhuma aresta;
  2. Para cada aresta e de G, se o grafo obtido por adicionar e a S é planar, então adicione e em S e classifique e como "planar" , senão rejeite e classifique como "não-planar" .

          Muitos algoritmos de desenho de grafos, sejam eles orientados ou não, podem ser encontrados em http://www.cs.brown.edu/people/rt/papers/gd-tutorial/gd-constraints.pdf .



<< Anterior   |   Índice   |   Próximo >>