



Next: Conclusões
Up: Modelos Contínuos
Previous: Experimentos Numéricos
Contents
Conclusões
Essa segunda parte do trabalho apresentamos uma metodologia, baseado em um problema de
decisão não-linear, para resolver o problema de empacotamento de retângulos em uma
região convexa. Os resultados numéricos mostram que essa metodologia é uma aproximação
promissora.
Os resultados mostram que para alguns problemas resultou em melhores resultados
(empacotou mais retângulos) em relação as soluções encontradas em [6], que
empacota retângulos inclinados.
Table:
Problemas e regiões.
|
Problema |
Região |
Objetos empacotados |
|
|
|
Dimensões |
nRet em [6] |
nRet |
| 1 |
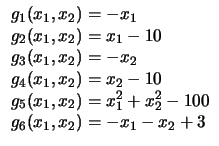 |
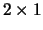 |
30 |
31 |
| 2 |
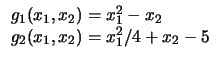 |
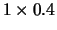 |
26 |
26 |
| 3 |
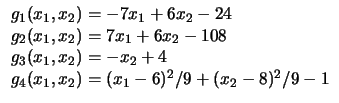 |
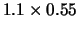 |
30 |
28 |
| 4 |
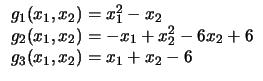 |
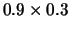 |
30 |
32 |
| 5 |
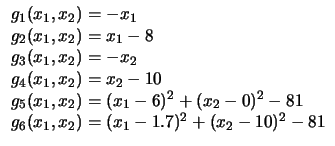 |
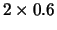 |
34 |
38 |
| 6 |
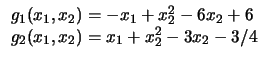 |
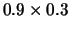 |
31 |
30 |
| 7 |
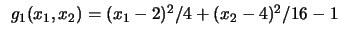 |
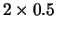 |
19 |
19 |
| 8 |
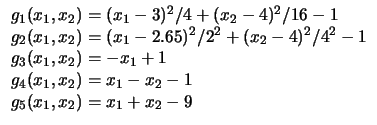 |
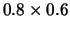 |
24 |
22 |
| 9 |
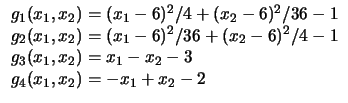 |
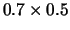 |
30 |
32 |
| 10 |
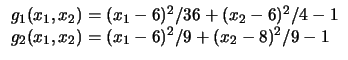 |
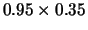 |
30 |
34 |
| 11 |
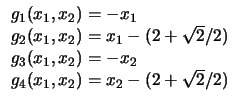 |
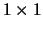 |
5 |
4 |
| 12 |
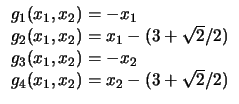 |
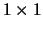 |
10 |
9 |
| 13 |
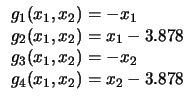 |
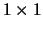 |
11 |
9 |
| 14 |
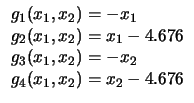 |
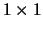 |
17 |
16 |
| 15 |
 |
 |
18 |
16 |
|
|
|
|
|
|
Table:
Problemas e regiões (continuação).
|
Problema |
Região |
Obejtos empacotados |
|
|
|
Dimensões |
nRet em [6] |
nRet |
| 16 |
 |
 |
19 |
16 |
| 17 |
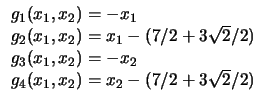 |
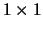 |
26 |
25 |
| 18 |
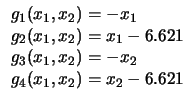 |
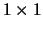 |
37 |
36 |
| 19 |
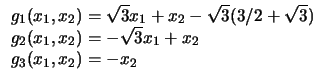 |
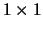 |
27 |
25 |
| 20 |
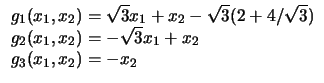 |
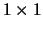 |
28 |
26 |
| 21 |
 |
 |
29 |
29 |
| 22 |
 |
 |
30 |
29 |
| 23 |
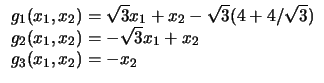 |
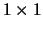 |
31 |
30 |
| 24 |
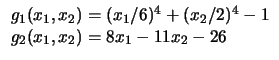 |
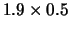 |
27 |
30 |
| 26 |
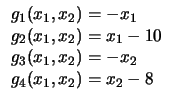 |
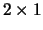 |
40 |
40 |
| 27 |
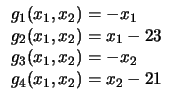 |
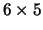 |
16 |
16 |
| 28 |
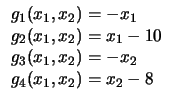 |
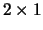 |
34 + 6 fixos |
34 + 6 fixos |
| 29 |
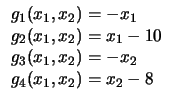 |
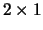 |
34 + 6 fixos |
34 + 6 fixos |
|
|
|
|
|
|
Table:
Problemas e regiões (continuação).
|
Problema |
Região |
Obejtos empacotados |
|
|
|
Dimensões |
nRet em [6] |
nRet |
| 31 |
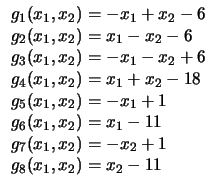 |
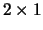 |
28 + 2 fixos |
28 + 2 fixos |
| 33 |
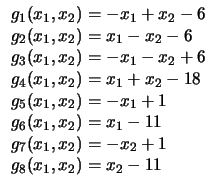 |
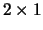 |
24 + 6 fixos |
24 + 6 fixos |
| 34 |
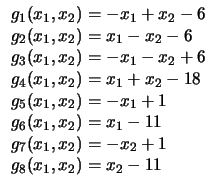 |
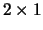 |
20 + 10 fixos |
20 + 10 fixos |
|
|
|
|
|
|
Figure:
(a-c) Restrições lineares e círculos,
(d-f) Restrições lineares e quadráticos (Problemas 1 a 6).
|
|
Figure:
Restrições lineares e elipses (Problemas 7 a 10).
|
|
Figure:
Quadrados em quadrados (Problemas 11 a 18).
![\includegraphics[]{fig/parte2/solucao/sol16.16}](img368.png) |
![\includegraphics[]{fig/parte2/solucao/sol26.26}](img369.png) |
|
| (a) |
(e) |
|
![\includegraphics[]{fig/parte2/solucao/sol17.17}](img370.png) |
![\includegraphics[]{fig/parte2/solucao/sol27.27}](img371.png) |
|
| (b) |
(f) |
|
![\includegraphics[]{fig/parte2/solucao/sol24.24}](img372.png) |
![\includegraphics[]{fig/parte2/solucao/sol28.28}](img373.png) |
|
| (c) |
(g) |
|
![\includegraphics[]{fig/parte2/solucao/sol25.25}](img374.png) |
![\includegraphics[]{fig/parte2/solucao/sol29.29}](img375.png) |
|
| (d) |
(h) |
|
|
Figure:
Quadrados em triângulos (Problemas 19 a 23).
|
|
Figure:
Curvas e restrições lineares (Problema 24).
|
|
Figure:
Retângulo em retângulo (Problemas 26 e 27).
![\includegraphics[]{fig/parte2/solucao/sol35.35}](img382.png) |
![\includegraphics[scale=0.7]{fig/parte2/solucao/sol34.34}](img383.png) |
| (a) |
(b) |
|
Figure:
Regiões proibidas para configurações especias em paletes (Problemas 28 a 34).
|
|




Next: Conclusões
Up: Modelos Contínuos
Previous: Experimentos Numéricos
Contents
Fabio Henrique Nishihara
2003-12-08